本文共 1130 字,大约阅读时间需要 3 分钟。
OBS 在 Windows 下的黑屏问题
系统环境
- 小米笔记本 Windows 10 Pro X-64
- OBS V22.0.2 64-bit
黑屏原因
为什么会黑屏呢?电脑硬件的原因? OBS 软件的原因?
首先,先来分析是否是电脑硬件的原因。下载 自带的直播软件,直播流程是可以完美走通的。这就排除了电脑硬件的问题。其次,是 OBS 软件的问题吗?自然不是,因为你总不是一个人在使用,类似于 OBS 这种优质的开源软件,修复 Bug 的速度是十分迅速的。现在,问题又回到了起点,究竟是什么原因导致的黑屏呢?
很幸运,在首次直播测试 OBS 的时候,碰到了,一个热心的小伙伴。他看到我在使用 Google Chrome 浏览器,就提出可能是 Chrome 设置的问题,是一种硬件加速的机制,如下图:

chrome-obs.png
只需要按照上图所示,关闭这两个选项就可以了。此时,关闭 Chrome ,打开 OBS 或许你的问题已经解决了,但是也可能仍旧黑屏,如果是这样,请继续往下看。
通过上述分析和操作,我们已经排除了电脑硬件和 OBS 软件的问题,但是问题没有得到良好解决,那就只可能是电脑配置的问题,而电脑上管理显示的组件就是显卡了。比如,小笔笔记本有独显和集显两个显卡, N 卡默认对 OBS 的显示配置是自动检测,通过测试我发现,确实如网上所查询的那般,只有使用集显的时候,才能够正确捕捉显示器及窗口,解决 OBS 黑屏的问题。
通过 控制面板/外观显示/ NVIDA 控制面板 或任务栏托管处打开 NVIDA 显卡的设置界面,如下图所示:
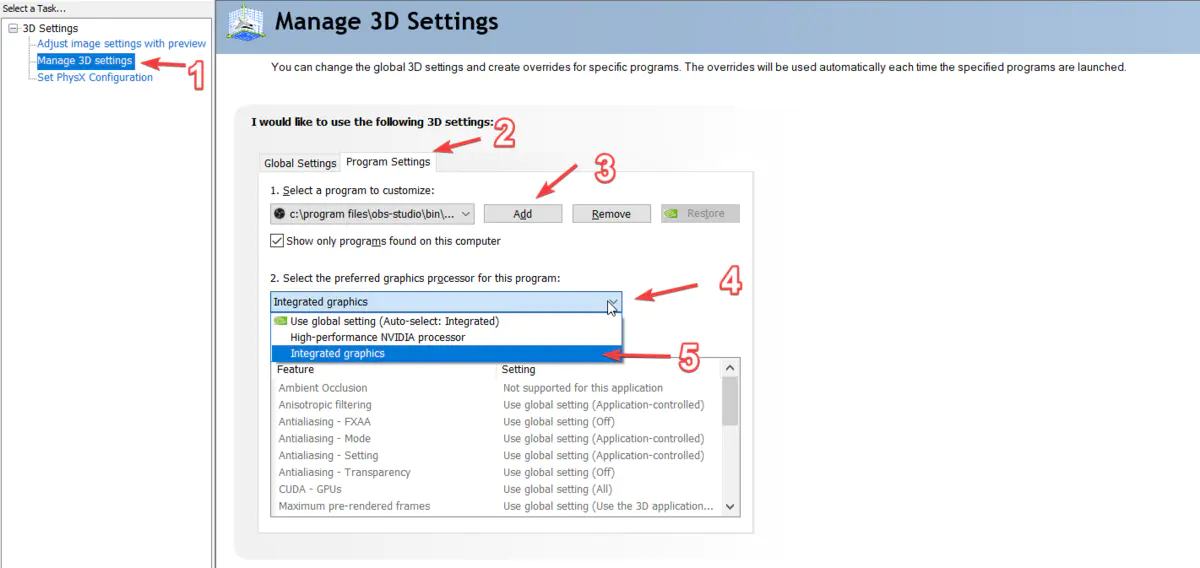
n-obs.png
按照上图所示步骤操作即可,其中第 3 步添加程序那一步,需要选择 OBS 程序,这样设置便只对 OBS 使用集显,其他软件仍然保持自动探测,比如休闲轻办公的时候使用集显,降低电脑发热,玩游戏的时候对显卡较高的时候,会自动切换为 N 卡,以提高游戏体验。
至此为止,在你看到这篇文章这个阶段,你用的 OBS 版本捕获显示器黑屏的问题已经解决了,重新启动 OBS 试一下吧,如果有必要的话,重启一下的电脑应该可以了。
另外,如果你用的 OBS 版本较久(不推荐使用旧版本),但你的电脑系统略新(如 win10),而上述方法,仍然无法捕获显示器和窗口,尝试一下兼容性运行,如下:
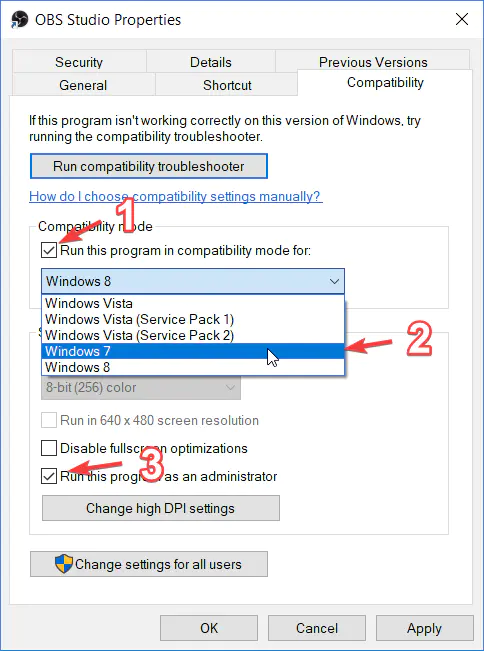
p-obs.png
至此,所有目前知道的解决办法都在这里了,如果还没有解决问题,那就善用搜索,找寻最新的解决办法吧。
作者:lovemininal 链接:https://www.jianshu.com/p/8709e779f444 来源:简书 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。